四角錐台の体積を計算する必要がありました。 上記公式に数字を当てはめるとA=43 B=36 a=29 b=19 h=18 単位cmです。 公式に当てはめて計算してみると大方18リットル=10升=?斗であることがわかりました。正四角錐の内接円の公式で 正四角錐出なくても使えますか? abcの1辺を2とする正三角形でoabcの四面体に内接する球の半径を求めよoa=ob=oc=4とする。公式通りなら表面積 abc=√3 oab体積=6 2 ×π×3√5÷3=36√5π(㎤) 円すいの体積の公式 底面積×高さ×1/3 正四角錐の体積 底辺の1辺が6cm 他の辺が9cmの四角すいの体積を考える 直角三角形OAHから三平方の定理を利用して高さOHを求めればよい。 まずAHの長さを求める

50 グレア 四角錐面積 壁紙配布
正四角錐 体積 公式
正四角錐 体積 公式-中1 数学 円錐・四角錐・正四角錐の公式 11 399 0 このノートについて 😭 答えは、表面積が528で、体積が2でした!正四角錐(せいしかくすい) 直錐である(頭頂点から底面への垂線が底面の重心を通る)方錐。いわゆる「ピラミッド型」である。しばしば斜錐の存在を考慮せず、方錐と正四角錐を同義と説明することがある。 斜方錐(しゃほうすい) 斜錐である方錐



この公式って存在しますか Clear
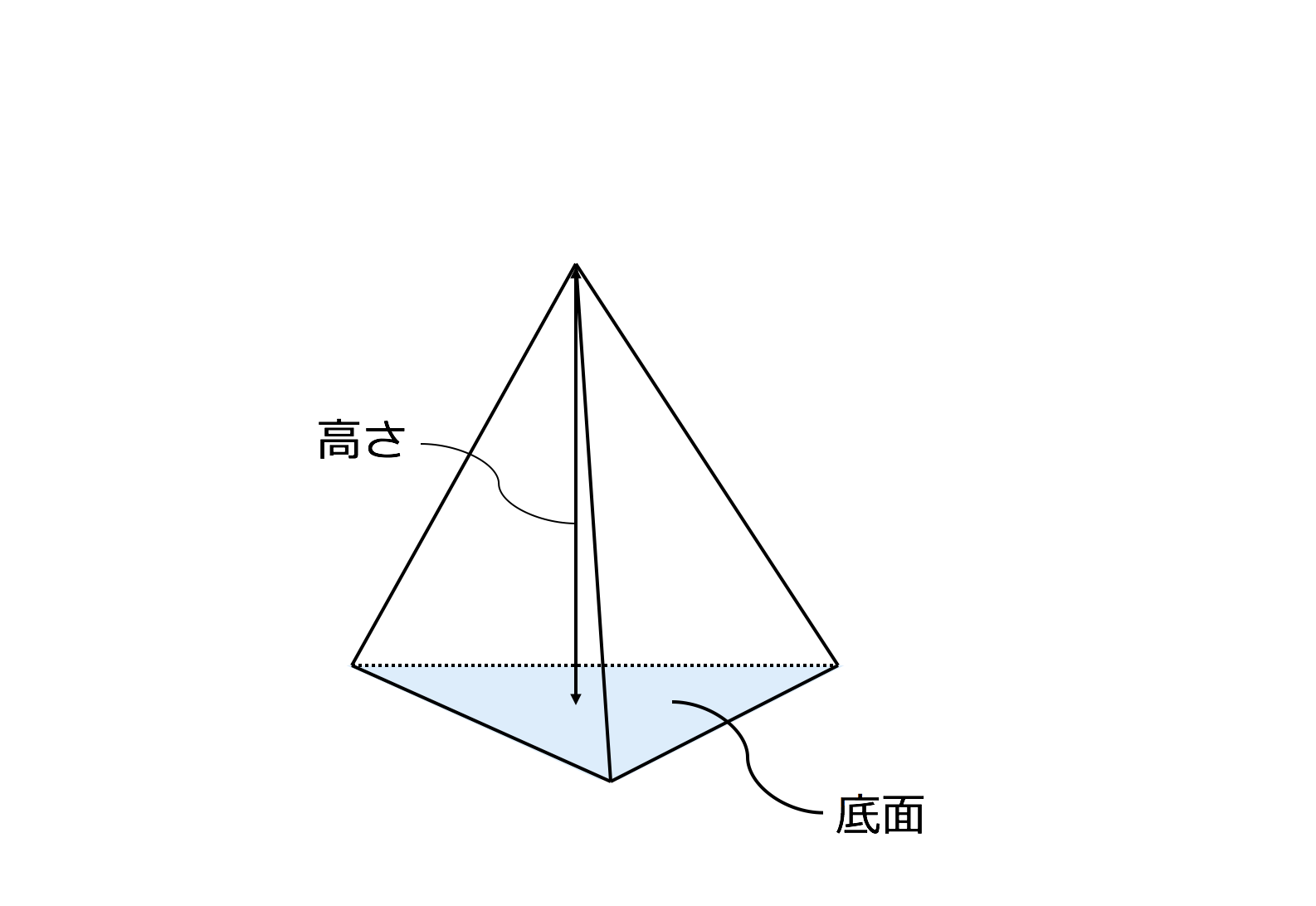
正四角錐の体積の求め方の公式って?? こんにちは!この記事をかいているKenだよ。青い空が好きだね。 正四角錐の体積の求め方には公式があるんだ。 正四角錐って底面が正方形で、先がとんがっている立体のことだったよね。長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は = となる。 任意の正四角錐は、適当な直交変換により、以下の方程式に変換できる。正四角錐abcde があります。辺acを 3:2 に内分する点をp,辺aeを 2:1 に内分する点をr として、 b,p,r を通る平面で切断し、平面bprと辺adの交点をq とします。 このとき、四角錐abpqr の体積は? 解答1 ベクトルを太字で表すことにします。
長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は = となる。 任意の正四角錐は、適当な直交変換により、以下の方程式に変換できる。すなわち、古代エジプト人は正四角錐台の正しい体積の公式を知っていたとわかる。高さを h、底面の辺を a、上面の辺を b とすると、次のような公式となる。 = ( ) 古代エジプト人がどのようにして正しい公式にたどり着いたのかは不明である。テンプレートInfobox Polyhedron with net 四角錐(しかくすい)とは、底面が四角形の錐体である。 底面が多角形なので、四角錐は角錐でもある。 種類 底面が長方形の四角錐を長方錐(ちょうほうすい)、その中でも底面が正方形の四角錐を方錐(ほうすい)と呼ぶ。
体積=6 2 ×π×3√5÷3=36√5π(㎤) 円すいの体積の公式 底面積×高さ×1/3 正四角錐の体積 底辺の1辺が6cm 他の辺が9cmの四角すいの体積を考える 直角三角形OAHから三平方の定理を利用して高さOHを求めればよい。 まずAHの長さを求めるAcは底面の正方形abcdの対角線なので ≫ 三平方の定理に当てはめて ac 2 =12 2 12 2 ac 2 =2 ac=±12 2 ac>0より ac=12 2 oからacに引いた垂線をomとすると これが四角錐の高さになる。 amはacの 1 2 なので am=6 2 ≫ o a c 15cm 15cm m 12 2 cm 6 2 cm oamで三平方の定理を使うと 15 2 =om正四角錐bdegの体積は,立方体abcdefghから,合同な4つの四角錐の体積を引くことで求められる。aを用いて,立方体abcdefghの体積は, ア cm3と表せ,四角錐abceの体積は, イ cm3と表せる。



四角錐台の斜辺の長さ Okwave



展開図 Qikeru 学びを楽しくわかりやすく Part 2
四角錐の体積の求め方公式 四角錐の体積を求める問題 問題① 《四角錐の体積の求め方》 問題② 《四角錐の体積の求め方》 問題③ 《四角錐の高さの求め方》 (adsbygoogle = windowadsbygoogle )push({});四角錐の体積の求め方公式 四角錐の体積を求める問題 問題① 《四角錐の体積の求め方》 問題② 《四角錐の体積の求め方》 問題③ 《四角錐の高さの求め方》 (adsbygoogle = windowadsbygoogle )push({});四角錐の表面積=底面積+側面積 であることから 求める四角錐の表面積=25+80=105(cm²)となります。 答え 105cm² 問題③ 次の四角錐の表面積を求めましょう。 《四角錐の表面積の求め方》 この四角錐の底面積=45×45=25(cm²)



図形計算機 Ease Labs



Nams出版プロジェクト 錐体の体積がなぜ1 3 3分の1 かを感覚的に納得させる方法
正四角錐台の体積 のことなんじゃないかな。 プリンみたいな立体だよ。 正四角錐台は台形の立体バージョンにみえるし、たぶんそう。。 そこで今日は台形の体積のかわりに、 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。この四面体の体積は, である. したがって,上の正四面体の体積は, 以上により, 1辺が の正四面体の体積は であることがわかった. 一般に,1辺が a の正四面体の体積を V とすると, だから, となる.体積がわかる! さて、正四面体の底面積、高さがわかりました。 あとは体積を求めて完了です。ここまでお疲れ様でした。 底面積 = $9\sqrt{3}$ 高さ= $2\sqrt{6}$ 三角錐の体積 = $底面積\times 高さ\times \frac{1}{3}$ 求める体積=正四面体の体積の半分



中2数学 中学数学に関する質問 勉強質問サイト



簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく
角錐・円錐の体積と表面積の公式 底面が1辺6cmの正方形、側面はすべて合同で底辺が6cm、高さが5cmの三角形の四角錐。また四角錐の高さは4cmとする。 正多面体の種類と性質一辺がxcmの正三角錐の体積の求め方がわかりません。 正三角錐の頂点をo底面を abcとします。正三角錐の高さは、頂点oと abcの重心を結んだ直線です。垂線(高さ)の足をh、bcの中点をdとします。hは重心なので、でした.これは三角錐でも四角錐でも,円錐でも使える公式です. この式に登場する \(\frac{1}{3}\)って何なの?という話をします. 三角形の面積と一緒?? 上に書いた錐の体積の公式とよく似た形の公式があることに気がつくでしょうか?



角錐に関する質問 3ページ 勉強質問サイト


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



台形 の 体積 計算 リタ ベルナル



1 と 2 の解き方と答え教えて下さい Clear



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ



錐の体積の公式 Youtube


Core Ac Uk Download Pdf Pdf



表面積の比と体積の比 中学数学に関する質問 勉強質問サイト



表面積に関する質問 3ページ 勉強質問サイト



角錐に関する質問 3ページ 勉強質問サイト


Core Ac Uk Download Pdf Pdf



相似な図形の問題です 中学数学に関する質問 勉強質問サイト



正八面体と球 Okwave



50 グレア 四角錐面積 壁紙配布



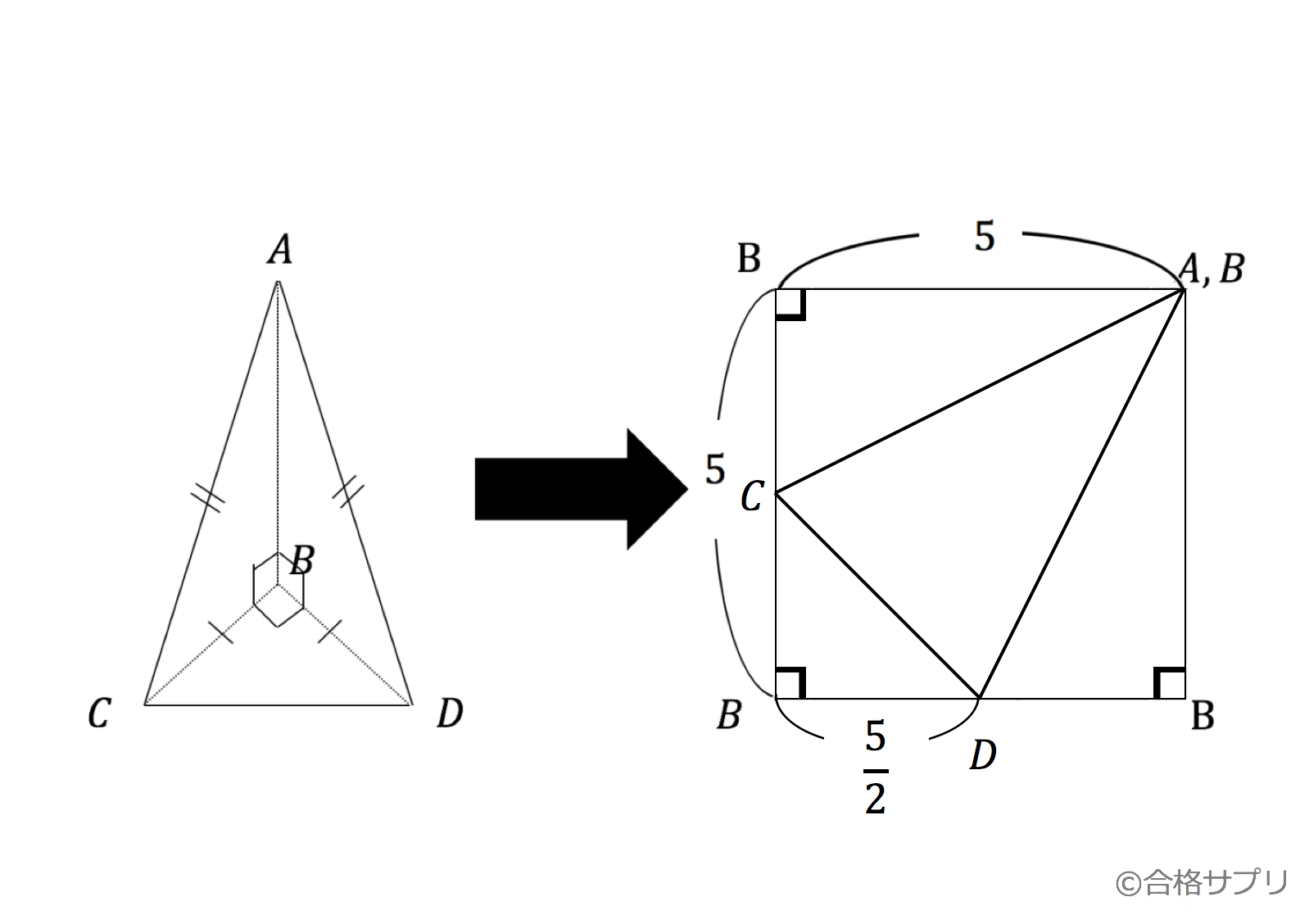
正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ


Www City Hadano Kanagawa Jp Www Contents Simple Kuukan481 Pdf



中3数学 正四角錐の高さと体積 5分で学習 Youtube



簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく



円錐や角錐の体積の求め方 中学1年数学 Youtube



Ppt 四角錐の体積 積分学まで待たねばならないか Powerpoint Presentation Id 7703



立方体公式 立方体计算 立方体体积 立方体英语



簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく



数学3 高校数学に関する質問 勉強質問サイト



なぜこうなるのか教えてください Clear


2



正四角錐の問題 高校数学に関する質問 勉強質問サイト


美しい 正四 角錐 体積 公式 壁紙 配布



数学3 高校数学に関する質問 勉強質問サイト



角錐に関する質問 3ページ 勉強質問サイト



錐体の表面積4 連問2円錐 円すいの体積と表面積の求め方 裏技公式 Youtube



56 四角錐の切断と体積 Youtube



優れた正四角錐公式 壁紙配布



壁紙押入れ ロイヤリティフリー角錐体積公式



三角錐の体積 積分学まで待たねばならないか Ppt Download



美しい 正四 角錐 体積 公式 壁紙 配布



Ppt 四角錐の体積 積分学まで待たねばならないか Powerpoint Presentation Id 7703



この公式って存在しますか Clear



錐体の表面積6 宿題解説 正四角錐の体積 表面積の求め方 Youtube



体積の比に関する質問 勉強質問サイト



立体の体積の求め方と公式 柱体 中学1年数学 Youtube


Http Www Tsumugi Ne Jp Member St3 74s Pdf



錐体の表面積1 例1正四角錐の表面積の求め方 Youtube



空間図形まとめ 数学 中学生 数学のノート Clear



この公式って存在しますか Clear


Core Ac Uk Download Pdf Pdf


Core Ac Uk Download Pdf Pdf



子供向けぬりえ 無料ダウンロード正四 角錐 公式



三平方の定理 覚えておきたい基本公式を解説 数スタ



5番を教えてください 早急にお願いします Clear


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



この三角錐の体積とその求め方を教えてください よろしくお願いします Clear



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ


イメージカタログ フレッシュ 四 角錐 展開 図 書き方
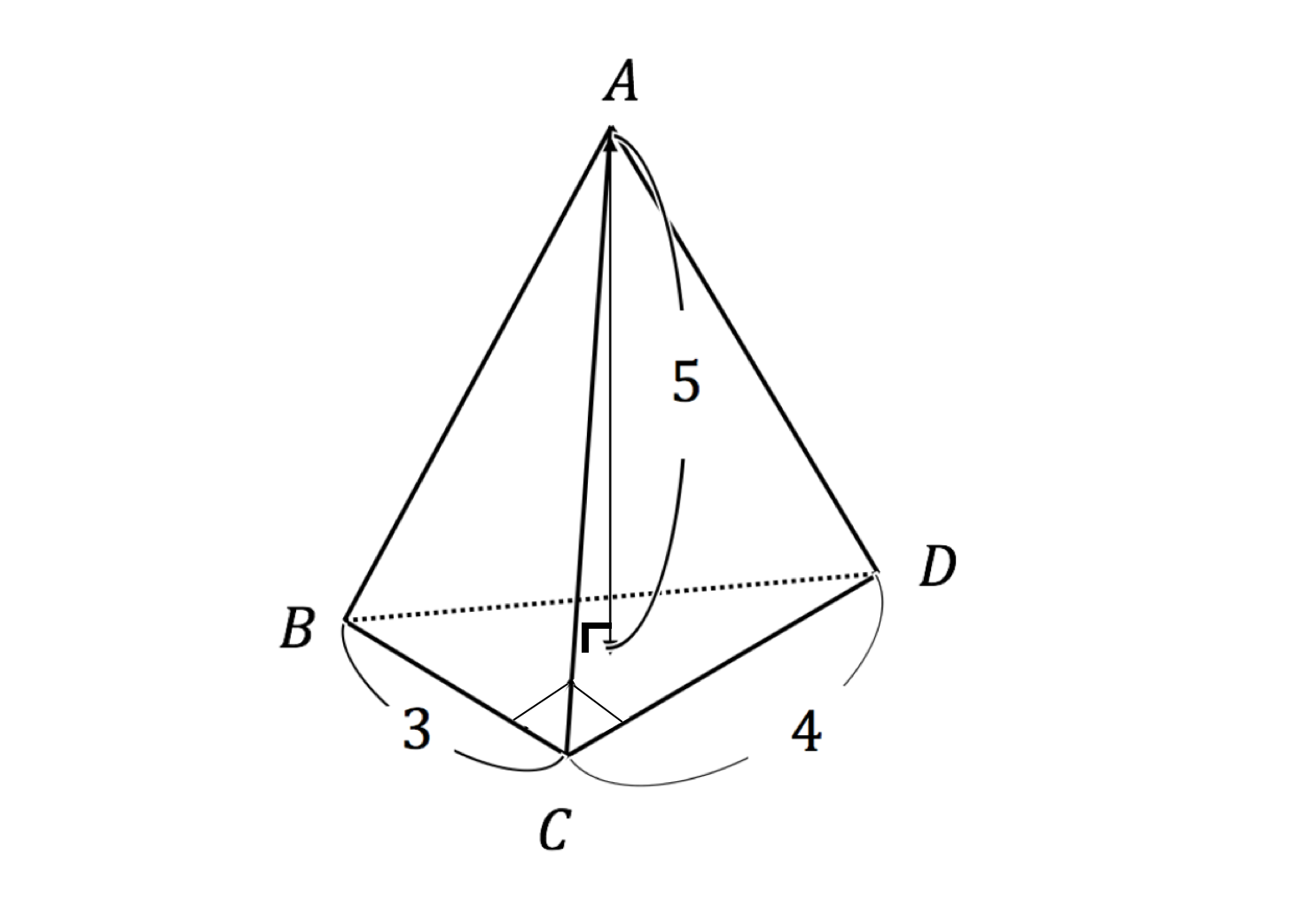


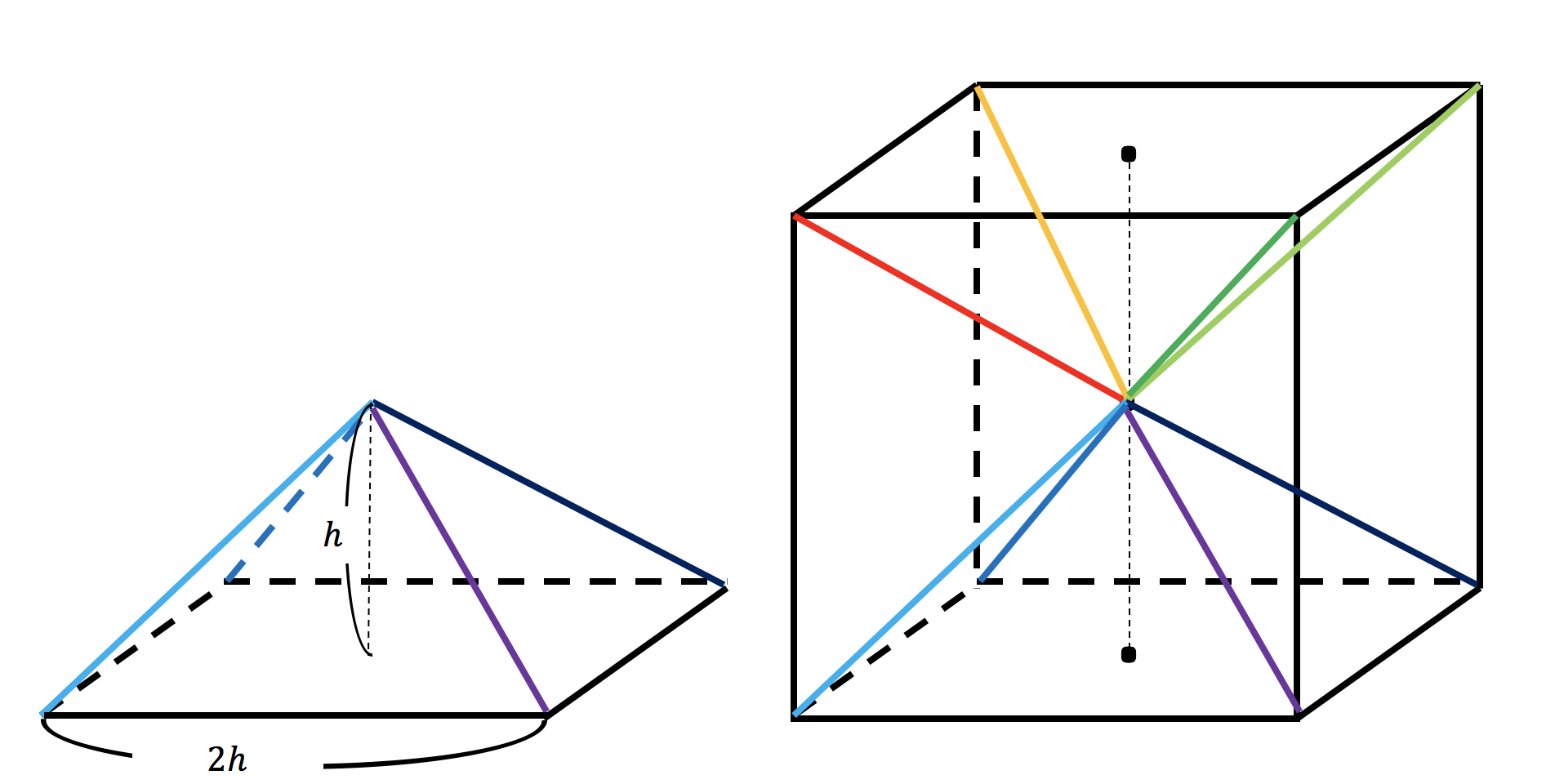
3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



物理 力学 物理に関する質問 勉強質問サイト



正四角錐o Abcdの体積をvとして 四角錐o Pqrsの体積が Clear



空間ベクトル 高校数学に関する質問 勉強質問サイト



50 グレア 四角錐面積 壁紙配布



子供向けぬりえ 無料ダウンロード正四 角錐 公式



この問題は一体どれなのでしょうか Clear



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ


無料ダウンロード立方体体積公式 ただぬりえ
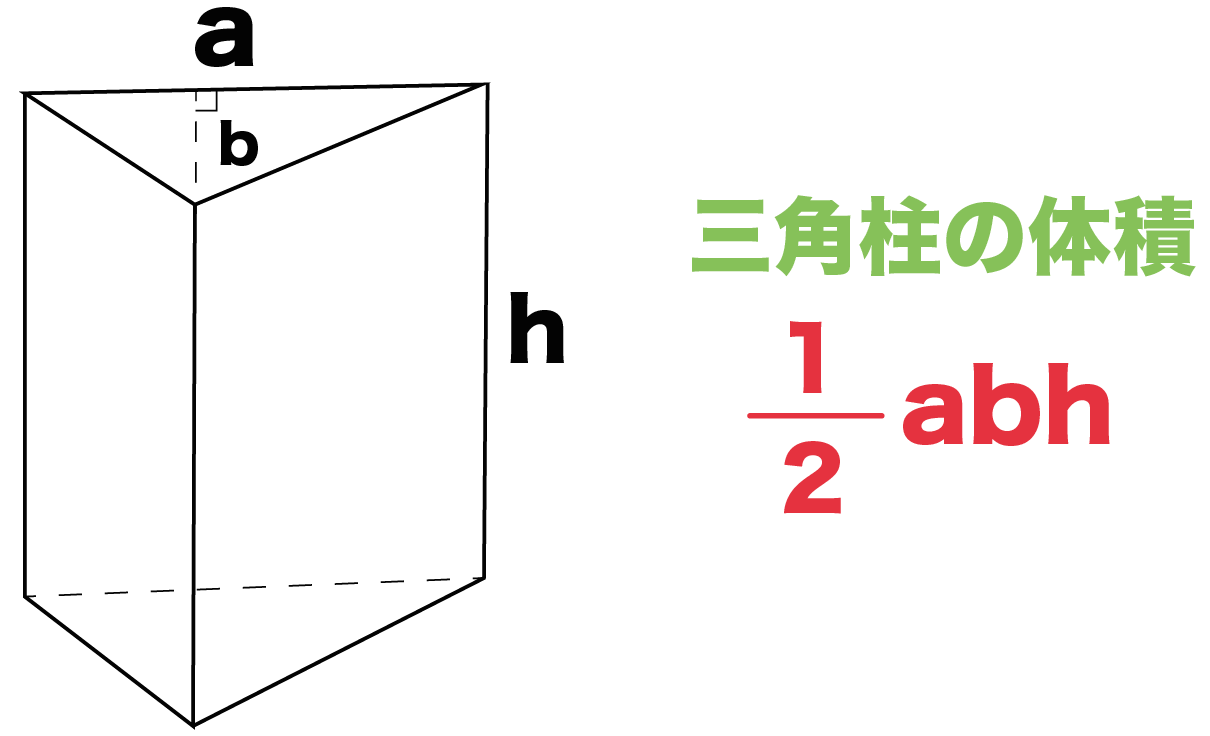


Qikeru 学びを楽しくわかりやすく Part 47



この正四角錐の体積を三平方の定理を使って求める途中式が分かりません Clear



子供向けぬりえ 無料ダウンロード正四 角錐 公式



この正四角錐の体積を三平方の定理を使って求める途中式が分かりません Clear



心に強く訴える角錐体積公式 ただぬりえ


塾 学校 家庭を結ぶ 受験情報サイト 学びネット



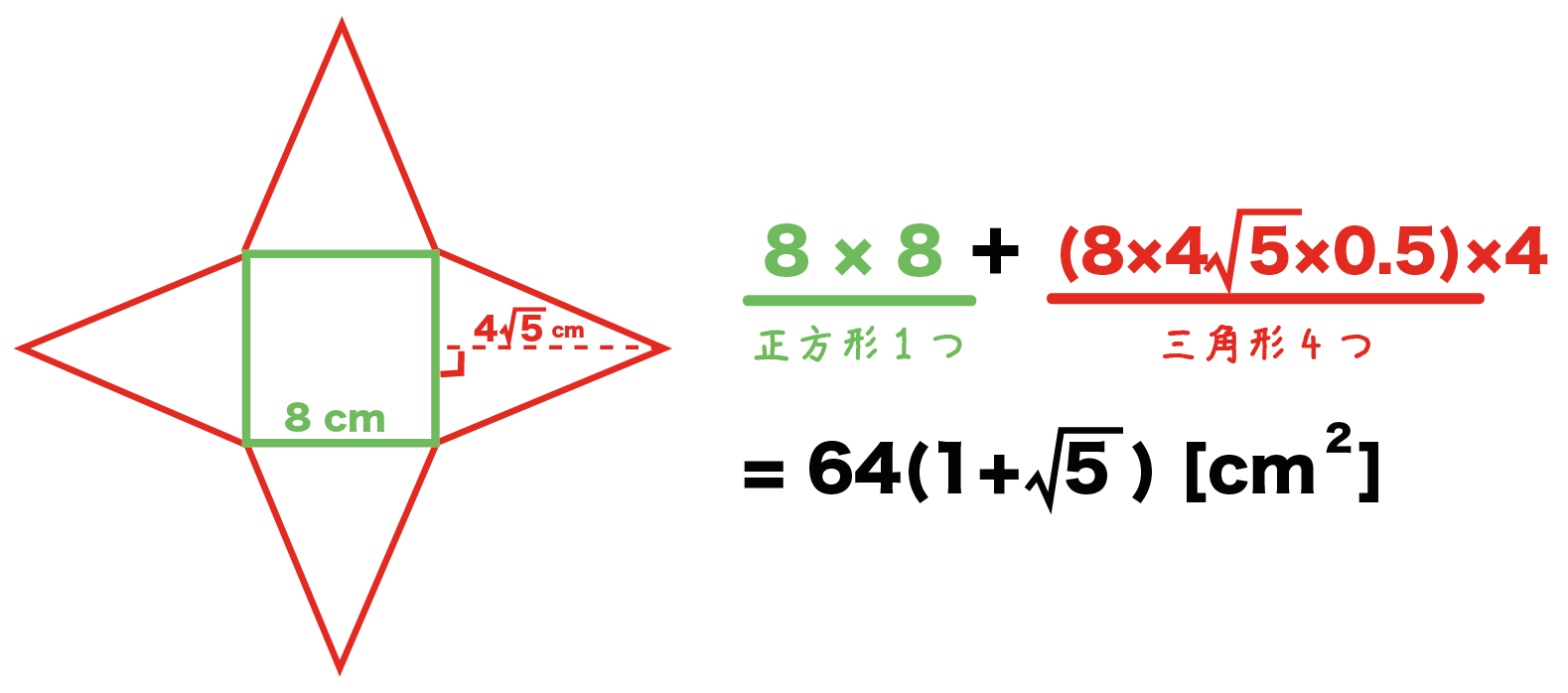
計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



ヤフオク 数学史 数学5000年の歩み 中村滋 室井和男


Service Zkai Co Jp Ad Muryoukyouzai C2 M Pdf
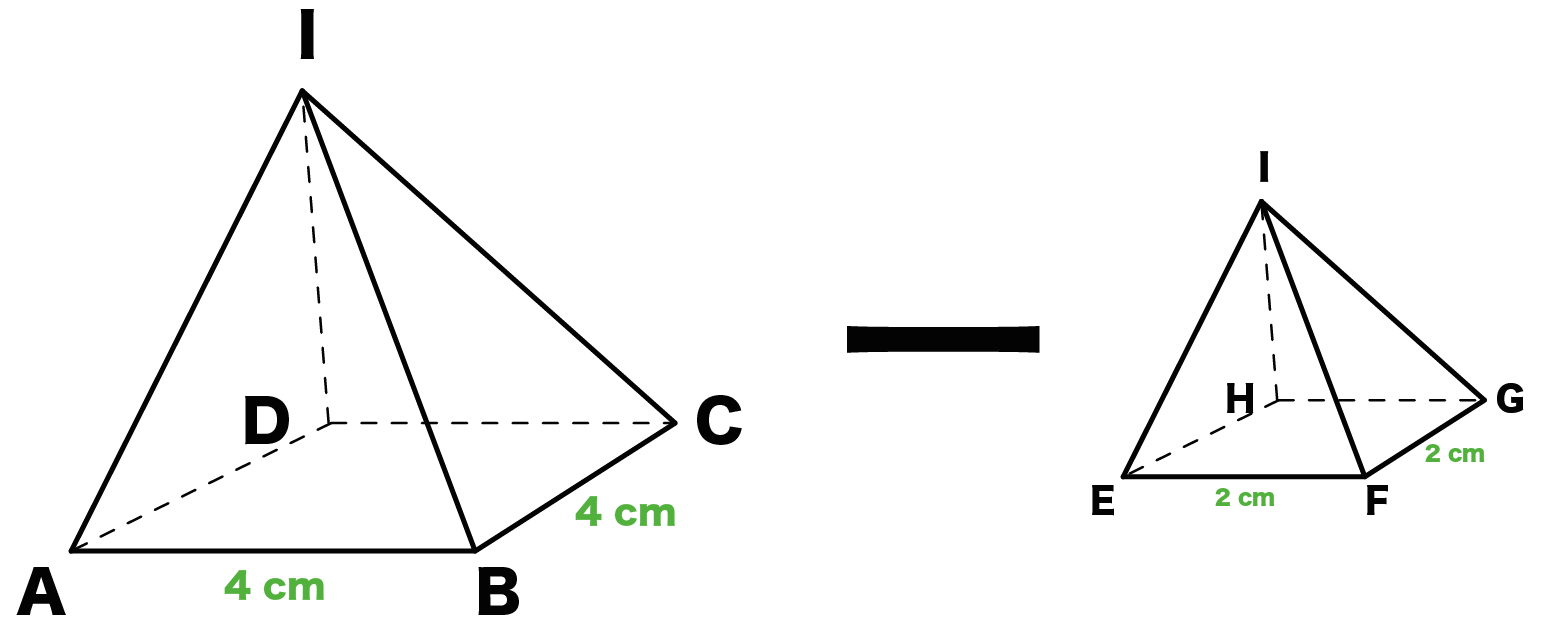


簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ


四角錐 Wikipedia


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



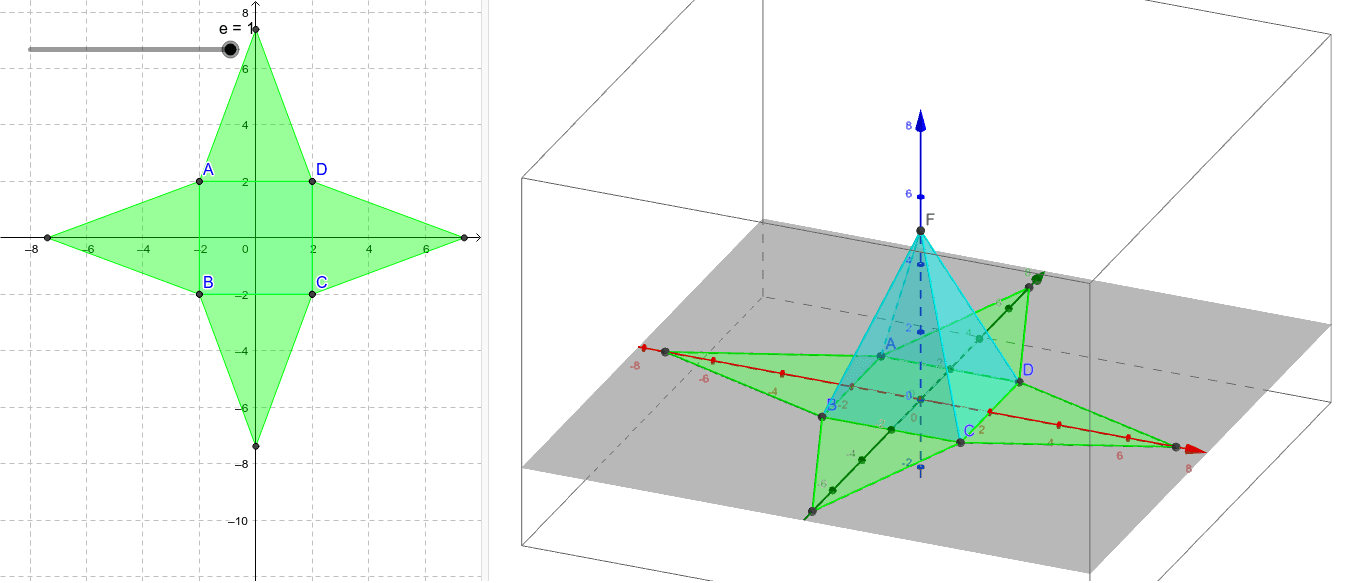
新しい 四 角錐 展開 図 書き方 アマゾンブックのポスト



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ


簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



子供向けぬりえ 無料ダウンロード正四 角錐 公式



角錐に関する質問 3ページ 勉強質問サイト
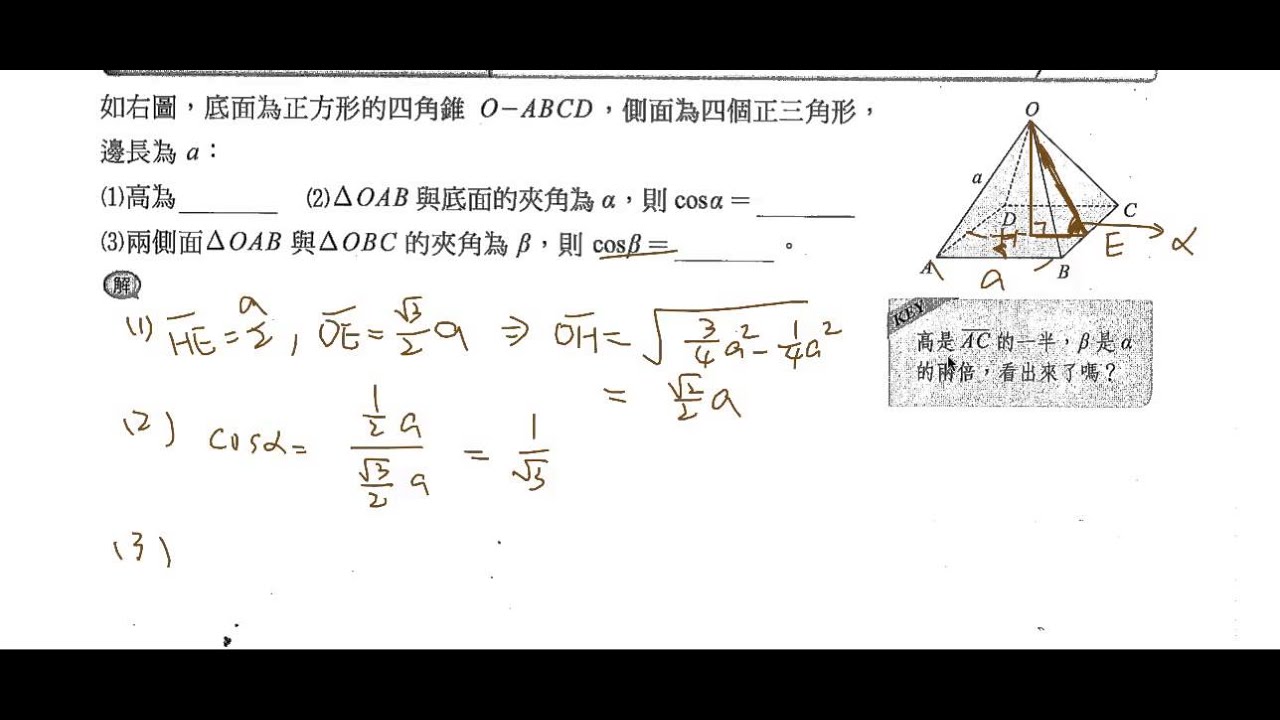


美しい 正四 角錐 体積 公式 壁紙 配布



角錐 円錐の体積 Youtube



子供向けぬりえ 無料ダウンロード正四 角錐 公式



数学 青チャートa 例題101 正四角錐の高さ 高校数学に関する質問 勉強質問サイト



โน ตของ 体積 表面積 側面積 の公式 ช น Junior Clear



高校数学a 正四角錐 正三角柱 正四面体 立方体の色の塗り分け 受験の月


Core Ac Uk Download Pdf Pdf


新しい 四 角錐 展開 図 書き方 アマゾンブックのポスト



Gkuiomhfmblaqm



数学3 高校数学に関する質問 勉強質問サイト



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ


