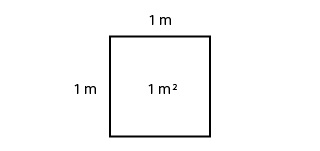
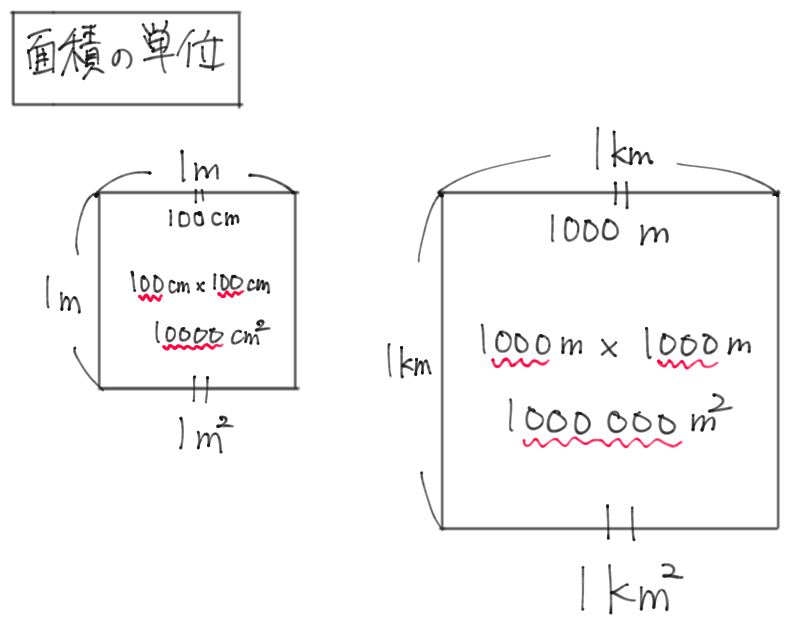
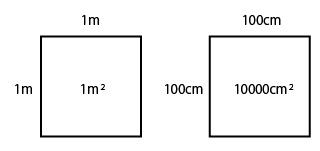
1㎡は、1辺の長さが1mの面積から、1㎡は何㎠か考えます。 1m=100cm なので 100×100=1 大きな面積の単位についての問題です。基本事項1辺の長さが1mの正方形の面積を1㎡(1平方メートル)といいます。1412= 1422= とうことは、 <a< 小数第三位を求めましょう。 とうことは、 <a< 小数第四位を求めましょう。 とうことは、 <a< 小数第五位を求めましょう。 とうことは、 <a< 問1 二乗すると9になる数は何ですか。何もかいていない方眼用紙を黒板に貼ります。そして、 先生「1マスが1㎠です。緑色の面積の大きさは、何㎠ですか。」 と、言いながら1㎠を貼ります。 あまりの、当たり前の問題に戸惑っていましたが。 子ども「1㎠です。」 無事に答えてくれました。

帖と畳の違いは 1帖って何 部屋の広さにまつわるあれこれ ひかリノベ スタッフブログ
1 は何分の何
1 は何分の何-今月の電気代は先月の電気代の何%ですか。 (解答) 5000 ÷ 4000=125 125=125(%) ※先月の電気代が基準なので、先月の電気代で割る。 (もし、「先月の電気代は今月の電気代の何%ですか」という問題ならば、 4000 ÷ 5000=08=80% と答えます。広さのことを面積といいます。 平方センチメートル(紙に書ける大きさなど) 面積は、1辺が1cmの正方形が何こ分あるかで表します。 1辺が1cmの正方形の面積を1㎠とかき, 「1平方(へいほう)センチメートル」とよみます。


1平方メートルは何平方センチメートル 1分でわかる意味と値 何メートル 何リットル
中1 数学 文字と式 G 1次式の計算 規則性の問題-授業プリント G1 下の図のように、マッチ棒をならべて正三角形を左から順に作っていく。このとき、次の問いに答えよ。 ⑴正三角形を5個作るには、マッチ棒は何本必要か。1名札は何㎠あるかなあ? 『あくしゅⅡ』№142(19,11,5) 面積を実感でとらえよう! 「面積の単位は?」 「ハーイ! 1㎠です」 「長方形の面積はどうやって求めるの?」 「たての長さ×よこの長さです」 「じゃあ、問題ね。気付かせ,1㎡が何㎠ になるのかという問い をもたせる。 ・前時で作った1㎡の正方形を提示し,実感を もって1mが何㎝か,1㎠ が何個敷き詰めら れるかを考えられるようにする。 ・長さの単位をそろえて面積を求めるだけでな
かげのついた図形の面積は何㎠ですか。 右の図で小さい (正方形) の面積が1㎠のとき ① は何こありますか。 ②右の長方形の面積は,何㎠ですか。 面積を求める公式を書きましょう。 ①長方形の面積= ②正方形の面積= 10分 /8 1 2 × 3 × ① ② ③ ④ ①1 ステップ1 三角形の等積変形① 1 下の図の直線アとイは平行です。このとき、辺BCを底辺とし、三角 形ABCと面積の等しい三角形を5つ、作図しなさい。直線アとイが 平行なことを利用して考えなさい。1辺が1mの正方形の面積を1㎡とかき, 「1平方メートル」と読みます。 1㎡=㎠ 平方キロメートル(町や県など) 1辺が1kmの正方形の面積を1㎢とかき, 「1平方キロメートル」と読みます。 1㎢=㎡ (1km=1000mです。
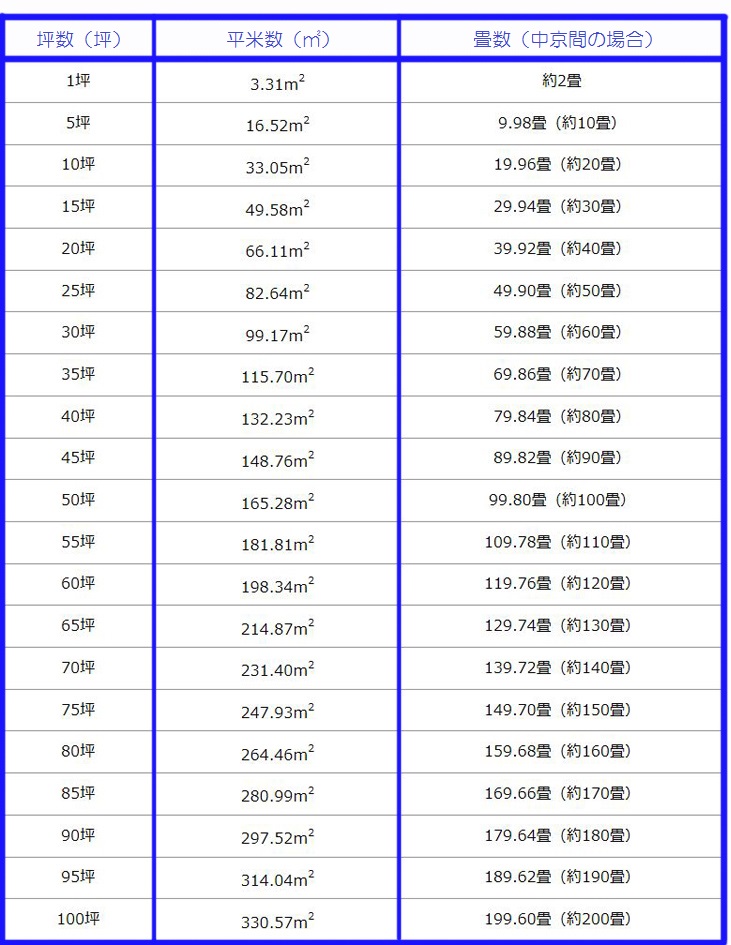
1㎡は、1辺の長さが1mの面積から、1㎡は何㎠か考えます。 1m=100cm なので 100×100=1 大きな面積の単位についての問題です。基本事項1辺の長さが1mの正方形の面積を1㎡(1平方メートル)といいます。1帖(1畳)=162m²とした場合、どのような計算式で「帖数」から「平米数」、またはその逆を求められるのでしょうか?見てみましょう。 例1、25m²は何帖か? 1帖(1畳)=162m²なので、 「平米数」を「162m²」で割れば、帖数が求められます。力 ・1㎡は何㎠になる ・1㎡の正方形に1 か調べる。 ㎠の正方形が何個 並ぶか調べ、1㎡ = ㎠である ことに気付けるよ うにする。 ・紙を使って、1㎡ ・新聞紙で実際に1 の正方形を作り面 ㎡の広さを作った 積の量感をつか り、その上に何人 む。



1畳って何平米 一人暮らしや二人暮らしにおすすめな畳数をご紹介 Chintai情報局


面積の単位 もう一度やり直しの算数 数学
・1 ㎡は何㎠になるか調べる。 ・紙を使って,1 ㎡の正方形を作 り面積の量感をつかむ活動に 取り組む。 知面積の単位㎡と㎠の 関係を理解してい る。 行動観察 ノート 発言(1) 斜線のついた部分の周りの長さは何cm ですか。 (2) 斜線のついた部分の面積は何㎠ですか。 3 次の図はそれぞれ、正方形と円またはおうぎ形を組み合わせた図形です。 (1) 図1の斜線部分の面積の合計は何㎠ですか。 8実践女子学園の入試問題問題(実践女子学園19) 右の図のように,同じ大きさの正方形が4つ並んでいます。太い折れ線の長さが cm のとき,正方形1つの面積は何㎠ですか。


1 は何 算数 大阪狭山市立東小学校


写真は1辺の長さが1cmの立方体の積み木を重ねた立体を 正面から見た図と真上か Yahoo 知恵袋
② 円周が通っている の部分を、1つ 約 05㎠とすると、面積は、約何㎠で 円の面積 = ×円周÷ すか。 は の 2分の1の大きさなので の数は17× =85 ( 85㎠ ) ③ 円の4分の1の面積は、約何㎠ですか。 69+ 85=775 ③ 半径51 1m3=何cm3=何L=何kl 5000cm3=何ml=何L 1L=何cm3=何mL 2 25dl=何dl 0024kL 043L=何ml 332kL=何L 5dl=何L 9100 3 問 内のりが縦2m、横3m、深さ2mの水槽があります。 容積は何Lですか。また、1時間に15tずつ 4 1km2=m2 = cm2 単位わかりますか 5 1000㎥は何kl1とても小さな「割合の単位」は? ppm(ピーピーエム) これは「100万分の1」という割合を表しています。つまり1 万分の1%です。1ppmを具体的にいうと、長さ25m、幅10m、 深さ1mのプールに溜めた水(250トン=250,000kg)に、コッ


1平方メートルは何平方センチメートル 1分でわかる意味と値 何メートル 何リットル


1 は何 算数 大阪狭山市立東小学校
② 半径1㎝の円が,右のような図形(かどはすべて直角です)の内側 を辺に沿って1周するとき,円の通る部分の面積は何㎠ですか。本郷 1辺の長さが5㎝の正方形ABCDを,右の図のように頂点Cを中 心に矢印の方向に回転しました。1. 右の図の四角形ABCDは長方形です。 黄緑の部分の面積は何cm 2 ですか。高さ(cm) 1 2 3 6cm 面積(㎠) 3 ②高さを cm,面積を ㎠として,底辺が6cm の三角形の面積を求める式を 書きましょう。 10 点 式( ) ③この三角形の面積が15 ㎠になるのは,高さが何cm のときですか。 5 点 ( ) ( ) ( ) ( ) ( ) ( )


分数の問題です 8こ分で1mになるはしたの長さ とは何ですか 息子 小学 Yahoo 知恵袋


1平米 は何坪 1坪は何平米 1畳は何坪 不動産の面積表示は ジューテックホームブログ
1412= 1422= とうことは、 <a< 小数第三位を求めましょう。 とうことは、 <a< 小数第四位を求めましょう。 とうことは、 <a< 小数第五位を求めましょう。 とうことは、 <a< 問1 二乗すると9になる数は何ですか。かげのついた図形の面積は何㎠ですか。 右の図で小さい (正方形) の面積が1㎠のとき ① は何こありますか。 ②右の長方形の面積は,何㎠ですか。 面積を求める公式を書きましょう。 ①長方形の面積= ②正方形の面積= 10分 /8 1 2 × 3 × ① ② ③ ④ ①かげのついた図形の面積は何㎠ですか。 右の図で小さい (正方形) の面積が1㎠のとき ① は何こありますか。 ②右の長方形の面積は,何㎠ですか。 面積を求める公式を書きましょう。 ①長方形の面積= ②正方形の面積= 10分 /8 1 2 × 3 × ① ② ③ ④ ①



100点塾 1リットルは何mlでしょうか



のやり方を途中式もお願いします Clear
1㎡は、1辺の長さが1mの面積から、1㎡は何㎠か考えます。 1m=100cm なので 100×100=1 大きな面積の単位についての問題です。基本事項1辺の長さが1mの正方形の面積を1㎡(1平方メートル)といいます。② 1辺が1㎝の正方形の面積を1㎠と書き,「1平 へい 方 ほう センチメートル」と読みます。 ③ 長方形や正方形の面積は,次の公 こう 式 しき で求められます。 長方形の面積=たて×横 正方形の面積=1辺×1辺1 2 次の長方形や正方形の面積は,何㎠ですか。 3 次の にあてはまる数を書きなさい。 1㎝ 1㎝ ㋑ ㋐ ① 広さのことを面 めん 積 せき といいます。 ② 1辺が1㎝の正方形の面積を1㎠と書き,「1平 へい 方 ほう センチメートル」と読みます。



小学5年生の算数学習アプリ Kidsapp Blog


日誌 横尾小学校
今月の電気代は先月の電気代の何%ですか。 (解答) 5000 ÷ 4000=125 125=125(%) ※先月の電気代が基準なので、先月の電気代で割る。 (もし、「先月の電気代は今月の電気代の何%ですか」という問題ならば、 4000 ÷ 5000=08=80% と答えます。ミリリットルとの関係 現在(1964年以降)では、1 mL(ミリリットル)は正確に 1 cm 3 である。 なお、1 cm 3 の水の質量は 約1 g(グラム)である。 1901年から1964年までは、「高精度測定のための体積の単位は, 最大密度で, 標準大気圧の下にある1 キログラムの純水によって占められる体積であり標準気圧(atmosphere、standard atmosphere) 760mmHg=760torr=101,325 Pa(= hPa) Pa (パスカル) SI(System International d'Unites)での圧力の単位はパスカルです。


1平方メートルは何平方センチメートル 1分でわかる意味と値 何メートル 何リットル


算数のコツ2 実はリットルと立方メートルの変換は暗記じゃない
高さ(cm) 1 2 3 6cm 面積(㎠) 3 ②高さを cm,面積を ㎠として,底辺が6cm の三角形の面積を求める式を 書きましょう。 10 点 式( ) ③この三角形の面積が15 ㎠になるのは,高さが何cm のときですか。 5 点 ( ) ( ) ( ) ( ) ( ) ( )1坪=3,3m2 1000坪×3,3=3300m2 正方形の面積1辺がXmの場合 X2=面積 √3300を開けば上記のように1辺の長さが出ます。ミリリットルとの関係 現在(1964年以降)では、1 mL(ミリリットル)は正確に 1 cm 3 である。 なお、1 cm 3 の水の質量は 約1 g(グラム)である。 1901年から1964年までは、「高精度測定のための体積の単位は, 最大密度で, 標準大気圧の下にある1 キログラムの純水によって占められる体積であり


帖と畳の違いは 1帖って何 部屋の広さにまつわるあれこれ ひかリノベ スタッフブログ



長方形の面積 たての長さ 横の長さ じゃない 算数を究める
平方メートル (へいほうメートル、square metre)は、 計量法 および 国際単位系 (SI) における 面積 の 単位 である。1 1平方メートルは、「辺の長さが一 メートル の 正方形 の面積」と定義される 。


これで単位換算は簡単 単位の暗記術 後編 中学受験プロ講師ブログ



算数 1 は何 100 子どもが覚える方法 Youtube



18平米の部屋は何畳くらい 広さや間取りのイメージを持っておこう Woman Chintai


算数の問題です 底面が1辺2 5cmの正方形である直方体の角材が Yahoo 知恵袋


子供の学校の宿題です すみません 添付問題の問2 問3の解き方 Yahoo 知恵袋


至急です 0 5平方メートルは何平方センチメートルですか 0 Yahoo 知恵袋


画像のように1組の三角定規を重ねて置くとき 斜線の部分の面積 Yahoo 知恵袋



1ヘクタールと1アール 面積はどのくらい 小学生 中学生の勉強



1平米 は何坪 1坪は何平米 1畳は何坪 不動産の面積表示は ジューテックホームブログ


10平方メートルとは 1分でわかる意味 計算 何平方センチメートル 一辺は何センチ


算数のコツ2 実はリットルと立方メートルの変換は暗記じゃない


残り12ページの割合がなぜ1 5分の1 1 4分の3になるのか Yahoo 知恵袋



帖と畳の違いは 1帖って何 部屋の広さにまつわるあれこれ ひかリノベ スタッフブログ


中学入試の過去問です 図のように 1辺が15cmの正方形の紙 Yahoo 知恵袋
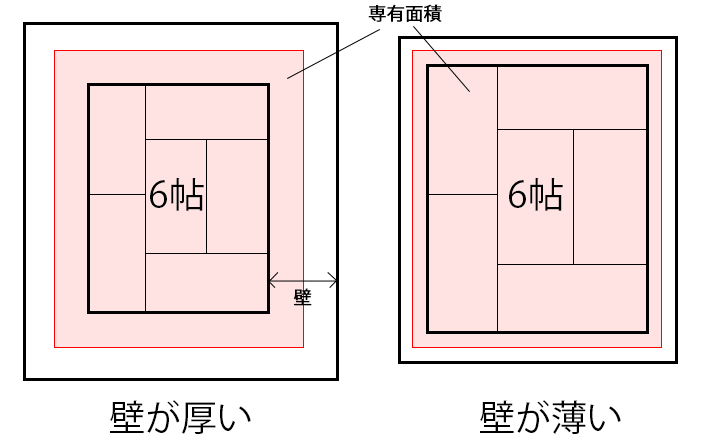


1帖 1畳 の広さ サイズってどのくらい 何平米



1ヘクタール 1ha は何アール 何平方メートル 不動産実務tips



ところで気密測定のc値ってなに 住宅の省エネ専門店 オカトミ
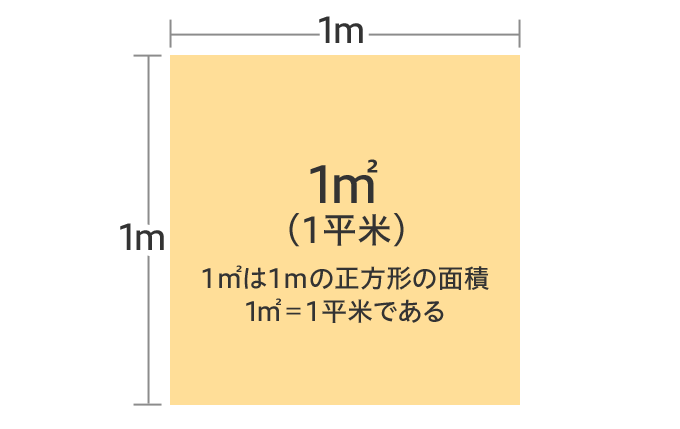


1平米の広さは 快適な生活には何平米必要 広さと間取りの基礎知識 スマイティ


小6算数です 3 と 4 の解き方を教えてください Yahoo 知恵袋


1 は何 算数 大阪狭山市立東小学校
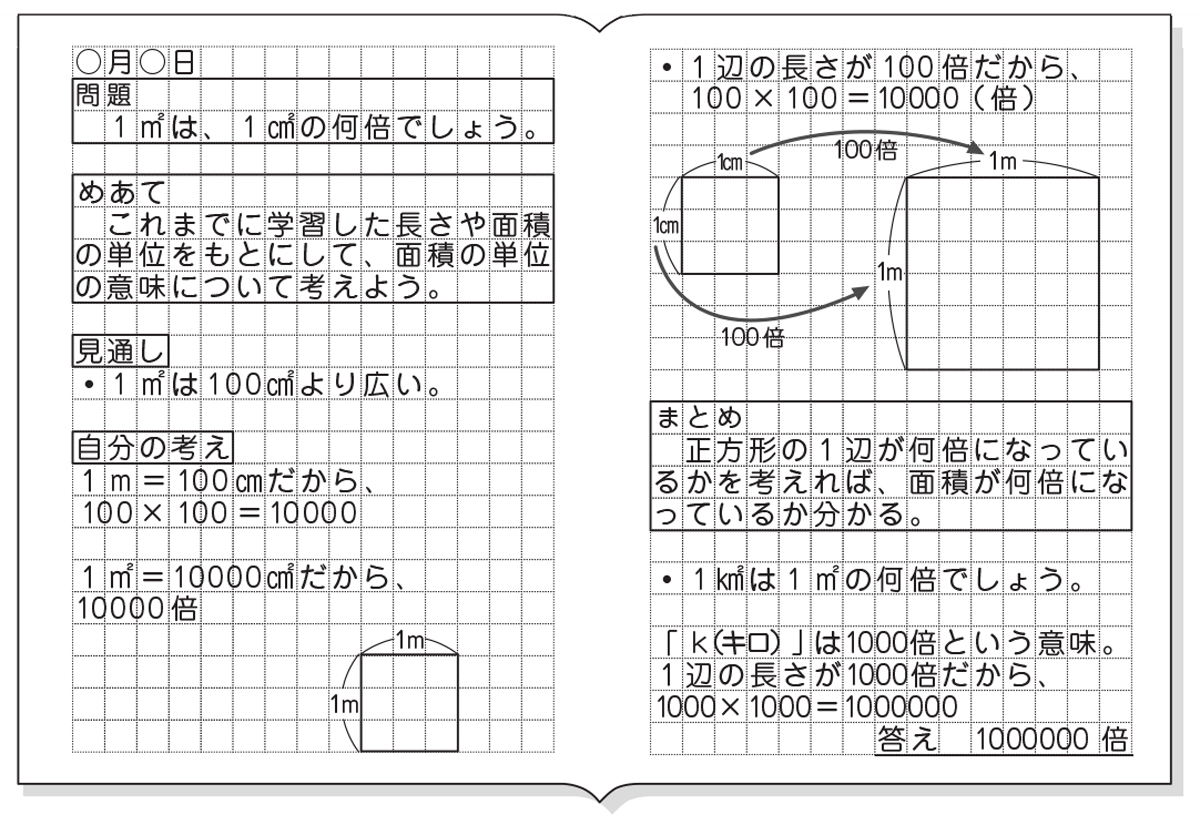


小学6年算数 量の単位 2 教科指導のヒントとアイデア みんなの教育技術



100m2ってmmに変換すると何桁ですか 100m2ってmmに変換すると何桁で 数学 教えて Goo


1cmは何mmですか 10mmです ついでに 1m メートル Yahoo 知恵袋
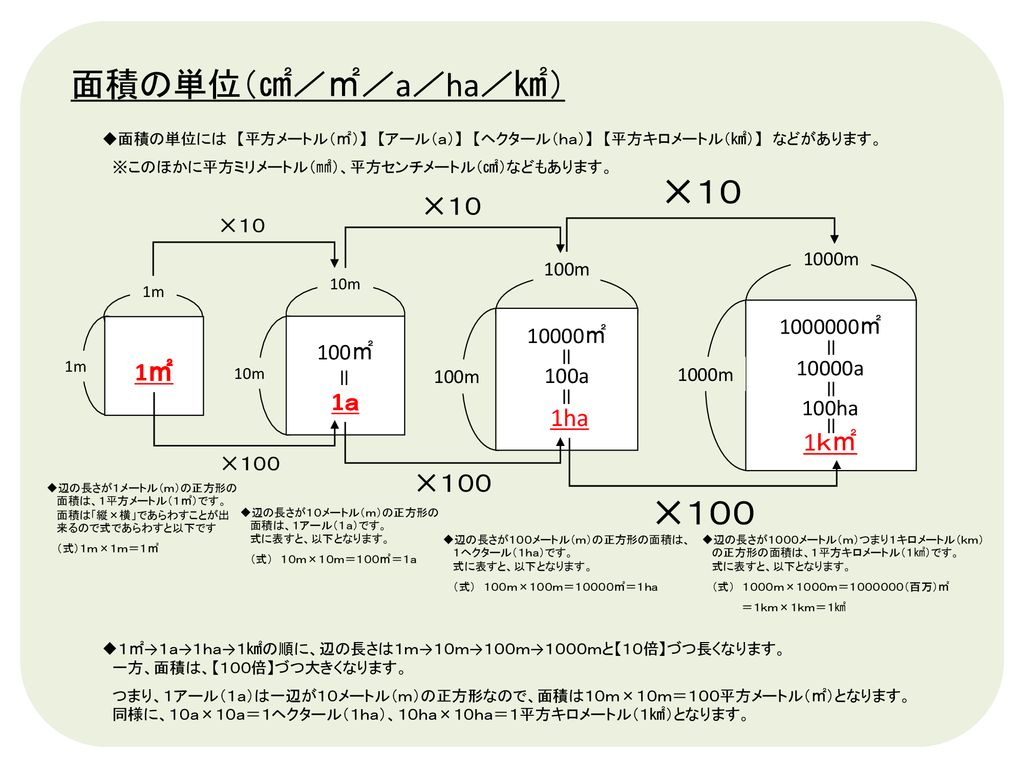


面積の単位 A Ha 1 1a 1ha 1k 100 a 100a 100ha Ppt Download



平米 の帖 坪への換算と広さや間取りの目安一覧 キーワードノート
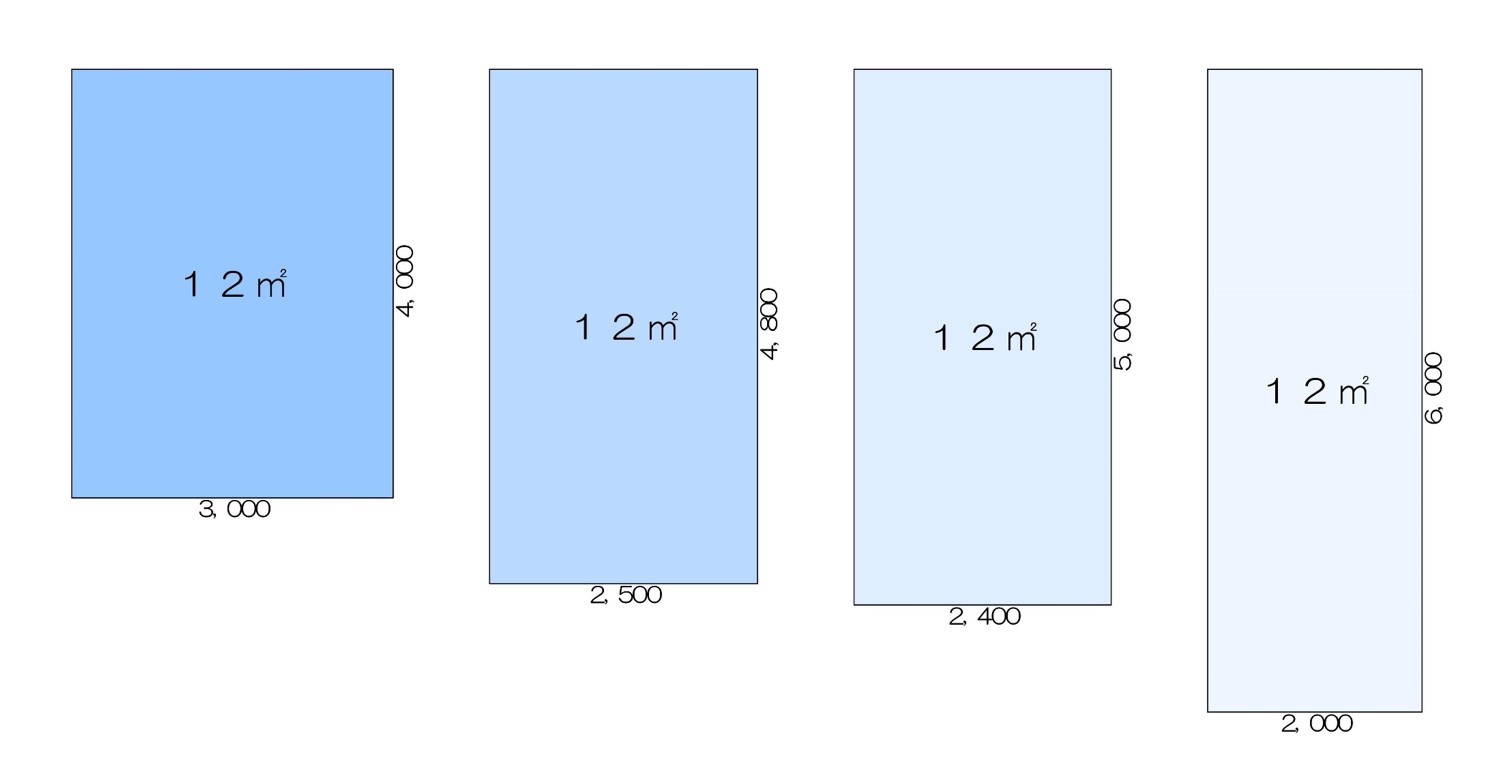


帖と畳の違いは 1帖って何 部屋の広さにまつわるあれこれ ひかリノベ スタッフブログ


帖と畳の違いは 1帖って何 部屋の広さにまつわるあれこれ ひかリノベ スタッフブログ



平面図形 算数に関する質問 勉強質問サイト


帖と畳の違いは 1帖って何 部屋の広さにまつわるあれこれ ひかリノベ スタッフブログ



1平方メートルは 何平方センチメートル リトル学習室 富士市岩松



小学校4年 面積 1平方センチメートルって何 面積シリーズ1 Youtube



全ての解説お願いします 特に最後の問題です Clear


長さ の 単位変換ツール ブラウザで使えるweb便利ツール



1ヘクタールと1アール 面積はどのくらい 小学生 中学生の勉強



ホームズ 0平米って何坪 何畳 どのくらいの広さ 具体的な間取りの例もご紹介 住まいのお役立ち情報



小学5年生の算数学習アプリ Kidsapp Blog
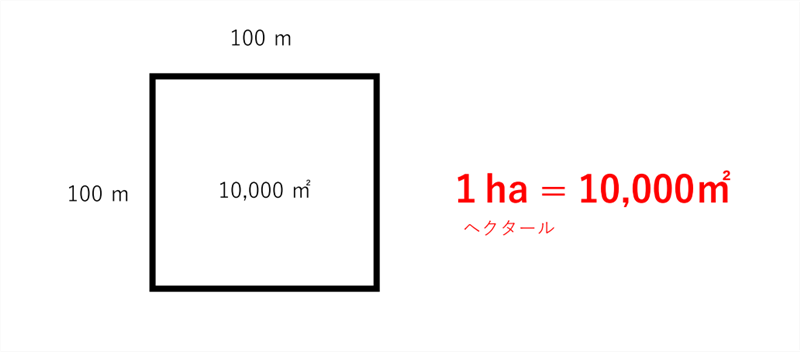


1ヘクタール 1ha は何アール 何平方メートル 不動産実務tips



1坪は何 平米 がわかる シニアの家間取り 理想の平屋を追求するブログ



1ヘクタール 1ha は何アール 何平方メートル 不動産実務tips



10平米の広さはどれ位 帖 坪への換算と間取りの目安 キーワードノート



大きな面積 平方メートルと平方センチメートル 練習 Youtube


面積の単位 もう一度やり直しの算数 数学
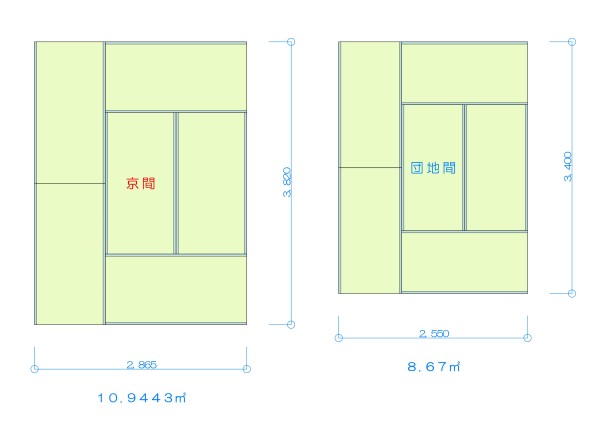


帖と畳の違いは 1帖って何 部屋の広さにまつわるあれこれ ひかリノベ スタッフブログ


算数の質問です 下の図において アと平行な面とイと平行な面で Yahoo 知恵袋



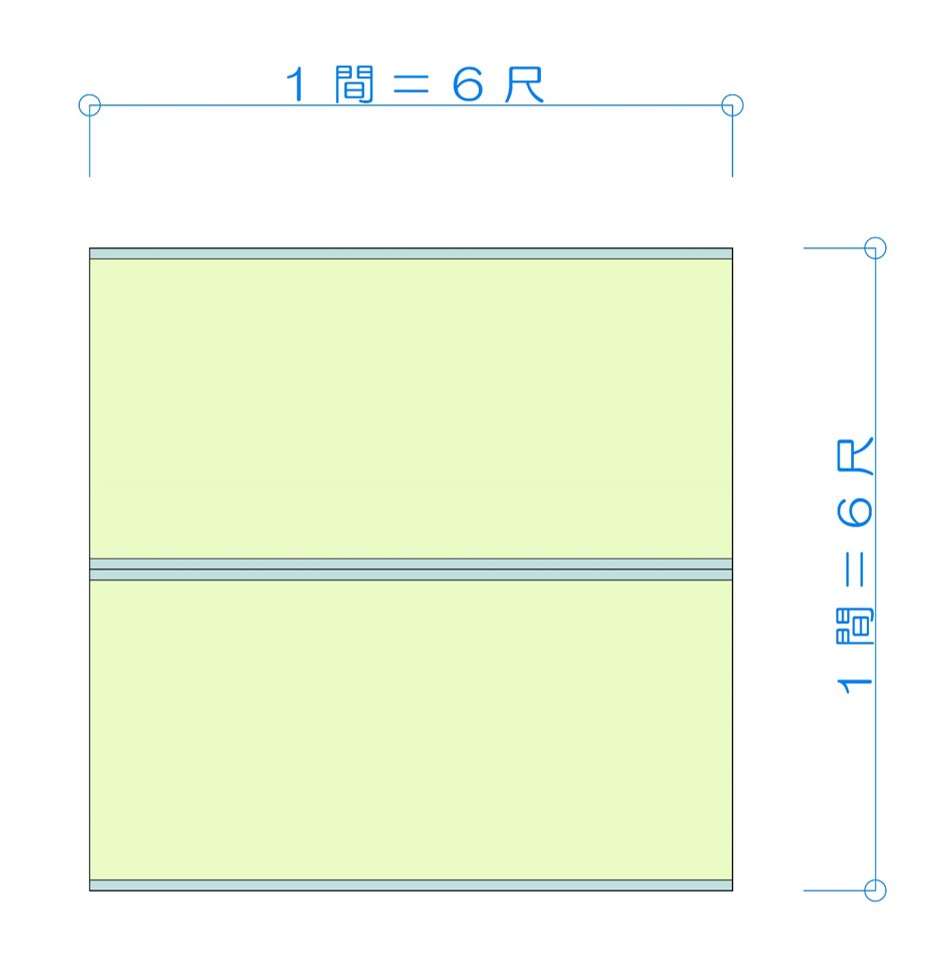
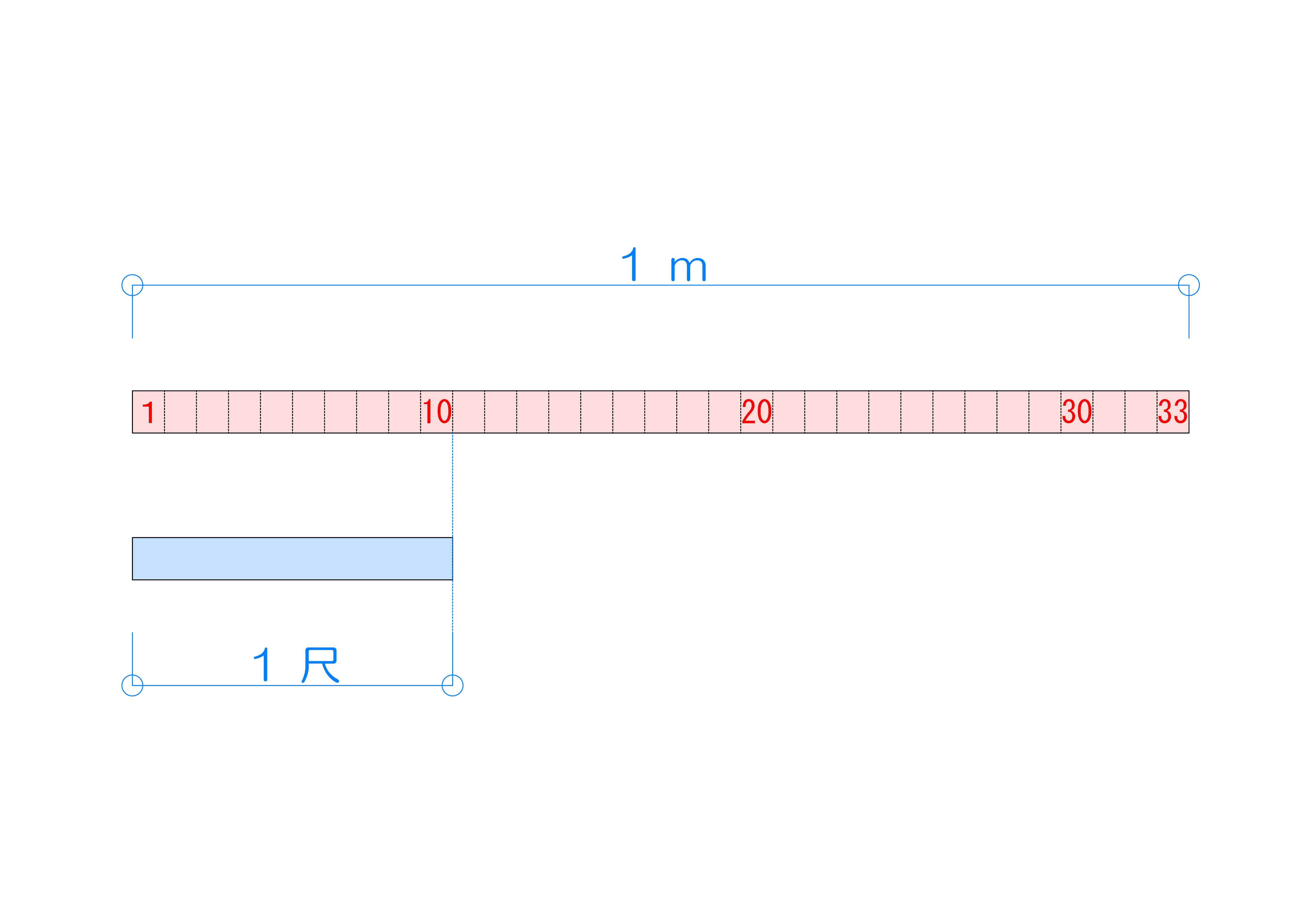
1間って何メートル 一坪って何帖 単位換算に困ったときの度量衡換算表 ほむせん
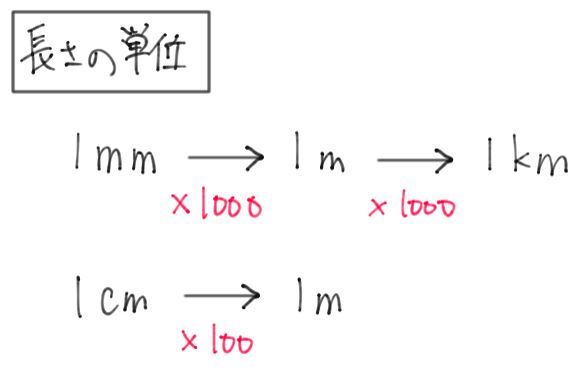


これで単位換算は簡単 単位の暗記術 後編 中学受験プロ講師ブログ



面積の単位 無料で使える学習ドリル



面積の単位 無料で使える学習ドリル



c 面 積 1c 広さのことを といいます 1辺が1cmの正方形の面積 面積は 1辺が1cmの正方形が いくつ分あるかで表します Ppt Download



帖と畳の違いは 1帖って何 部屋の広さにまつわるあれこれ ひかリノベ スタッフブログ
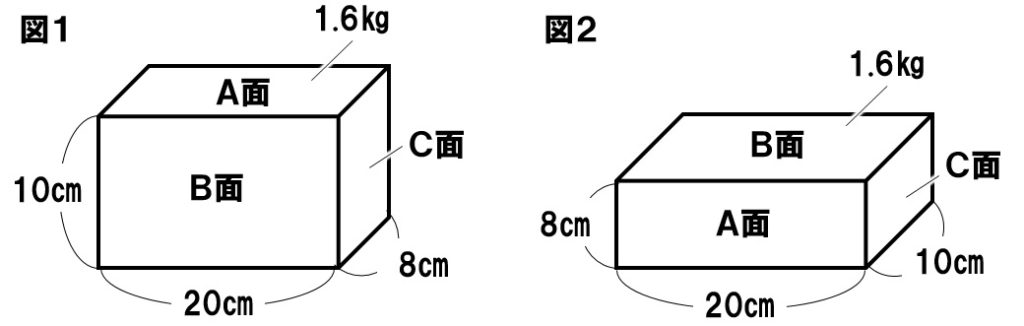


問題 圧力の計算 Examee



単位のまとめ 無料で使える学習ドリル


